Goniometrie, of hoekenmeetkunde, wordt in het Engels ook wel “trig” genoemd. Dat staat voor trigonometrie, of driehoekenmeetkunde. Zoals de naam al aangeeft gaat het over hoeken en driehoeken. Het wordt vaak als een lastig onderwerp gezien, voornamelijk omdat er functies met moeilijke namen (sinus, cosinus, tangens) en Griekse letters (\(\alpha\), \(\beta\), etc.) worden gebruikt. Alles wat je moet kennen voor het eindexamen VWO is echter op een A4-tje samen te vatten: Goniometrie-Samenvatting-VWO-Eindexamen.pdf.
Ik zal hier niet alle goniometrie voor het VWO beschrijven, dat kan beter uitgespreid worden over meerdere posts. In deze post behandel ik alleen de basis.
Eenheidscirkel
Goniometrie gaat over hoeken en driehoeken, dus beginnen we met: een cirkel? Een vorm die juist helemaal geen hoeken heeft?

Dit is misschien niet zoals goniometrie aan je is uitgelegd op school, maar we gebruiken deze cirkel zodat we goniometrie kunnen uitleggen met behulp van andere wiskundige begrippen die je al kent. Als je dit plaatje kent en snapt dan heb je het grootste gedeelte van goniometrie al onder de knie. Dus laten we dit plaatje eens beter bekijken.
We hebben een assenstelsel met een eenheidscirkel; een cirkel met straal 1 en een middelpunt dat op de oorsprong van het assenstelsel ligt. Er is ook een lijnstuk van de oorsprong naar de cirkel, en de hoek tussen de x-as en dat lijnstuk noemen we in deze tekening \(\alpha\), dat is de hoek waar we in geïnteresseerd zijn.
In de tekening zijn ook nog twee interessante punten: punt \(A\) is het punt waar het lijnstuk de cirkel snijdt, en punt \(B\) is het punt op de x-as dat we krijgen als we een rechtzijdige driehoek \(OAB\) maken.
Sinus en Cosinus
Met deze tekening en de driehoek \(OAB\) kunnen we de goniometrische functies definiëren. We weten dat \(OA = 1\), het lijnstuk gaat immers van de oorsprong naar de cirkel, en de cirkel heeft straal 1. De andere zijdes van de driehoek weten we echter niet; die hangen af van de hoek \(\alpha\), maar we kunnen zeggen dat we functies hebben (sinus en cosinus, of \(\sin\) en \(\cos\)) die de zijdes voor ons uitrekenen. Dus \(AB=\sin(\alpha)\) en \(OB=\cos(\alpha)\).
Meestal worden de haakjes weggelaten bij de goniometrische functies. Dus in plaats van \(AB=\sin(\alpha)\) en \(OB=\cos(\alpha)\) schrijven we vaak \(AB=\sin \alpha\) en \(OB=\cos \alpha\)
De formules voor de sinus en cosinus zijn best ingewikkeld en hoef je niet te kennen, het is genoeg om de definitie te kennen, en te weten dat er een knopje op je rekenmachine zit om ze uit te rekenen1In feite zijn ze zo ingewikkeld dat mensen voordat er rekenmachines waren vaak een goniotafel, d.w.z. een grote tabel in een speciaal boek, gebruikten om de waardes op te zoeken in plaats van ze uit te rekenen..
Merk op dat de coordinaten van punt \(A\) gelijk zijn aan de de lengte van de zijdes van de driehoek. Dus \(A = (\cos \alpha, \sin \alpha)\). Dus je kunt de sinus en cosinus niet alleen gebruiken om de zijdes van de driehoek uit te rekenen, maar ook de coördinaten van punt \(A\)2Om te onthouden of de cosinus of de sinus de x of de y coordinaat oplevert, denk ik altijd aan ijs; de Y-coordinaat is de Sinus..
Je kunt de sinus en cosinus functies omdraaien (inverteren) om gegeven de lengte van een zijde van de driehoek (of coördinaat van punt \(A\)) de hoek \(\alpha\) uit te rekenen. Ook hier zit een knopje voor op je rekenmachine. Op de meeste rekenmachhines staat er op dat knopje zoiets als \(\sin^{-1}\) en \(\cos^{-1}\) (waarbij de “tot de macht min een” wordt gebruikt om het omgekeerd aan te geven), of \(asin\) en \(acos\) wat staat voor arcsinus en arccosinus (denk hierbij dat de “a” staat voor “anti” of de omgekeerde functie).
Tangens
Er is nog iets interessants in de tekening: de richtingscoëfficiënt van lijnstuk \(AB\). Deze richtingscoëfficiënt hang ook van hoek \(\alpha\) af en om die uit te rekenen hebben we de goniometrische functie tangens of \(\tan\).
Je hebt de tangens echter niet vaak nodig; als je de zijdes \(AB\) en \(OB\) van de driehoek weet dan kun je de richtingscoëfficiënt namelijk uitrekenen zoals je dat eerder geleerd hebt:
\[\tan \alpha = \frac{AB}{OB} = \frac{\sin \alpha}{\cos \alpha}\]
Vaak wordt verwacht dat je deze formule uit je hoofd leert, maar als je de tekening kent, en weet hoe je een richtingscoëfficiënt uitrekent, dan snap je waar de formule vandaan komt en is het niet echt nodig/moeilijk meer om ‘m uit je hoofd te leren.
Overigens gebruik ik deze formule altijd zo snel mogelijk in een opgave. In de meeste goniometrie opgaves kun je de tangens hiermee namelijk vervangen door een breuk met sinus en cosinus erin, en daarmee de opgave verder oplossen. Daardoor hoef je verder niet veel uit je hoofd te leren wat betreft de tangens.
Pythagoras
Nog zo’n truc is de stelling van Pythagoras. De driehoek \(OAB\) is een rechtzijdige driehoek, en dus geldt de stelling van Pythagoras:
\(AB^2 + OB^2 = OA^2\) ofwel: \[(\sin \alpha)^2 + (\cos \alpha)^2 = 1\]
Ook dit is weer een formule waarvan wordt verwacht dat je ‘m uit je hoofd leert, maar als je de tekening kent, en de stelling van Pythagoras, dan snap je waar de formule vandaan komt en is het niet echt nodig/moeilijk meer om ‘m uit je hoofd te leren.
Ook hier geldt overigens weer dat wiskundigen vaak de haakjes weglaten bij goniometrische functies en dus \((\sin \alpha)^2 + (\cos \alpha)^2 = 1\) vaak schrijven als: \[\sin^2 \alpha + \cos^2 \alpha = 1\]
Daarbij zetten ze het kwadraat dus bij de functie om aan te geven dat het resultaat van de sinus of cosinus wordt gekwadrateerd, en niet de hoek.
Radialen in plaats van graden
Je bent misschien gewend om hoeken te meten in graden: 360 graden is een volledige cirkel, en 90 graden is een rechte hoek. Bij goniometrie gebruiken we echter vaak radialen in plaats van graden.
De afstand van punt \((1,0)\) naar punt \(A\) over de eenheidscirkel, tegen de klok in, is de grootte van de hoek \(\alpha\) in radialen.
De omtrek van de eenheidscirkel is \(2\pi\), dus een volledige cirkel is \(2\pi\) radialen, en een rechte hoek is \(\frac{1}{2}\pi\) radialen. Het omrekenen van een hoek in graden (\(\alpha_g\)) naar een hoek in radialen (\(\alpha_r\)) gaat als volgt:
\[\alpha_r = \frac{\alpha_g}{360} 2 \pi\]
Let erop dat je je rekenmachine in de juiste stand zet als je goniometrie opgaves doet. Als je rekenmachines hoeken in radialen verwacht maar je vult ze in graden in, of andersom, dan zal de uitkomst niet kloppen en loop je punten mis.
Samenvatting
En dat is alles uit deze tekening. Met deze informatie hebben we de sinus, cosinus en tangens gedefinieerd en gekoppeld aan dingen waar je al bekend mee bent: de lengte van de zijdes van een driehoek, coördinaten in een assenstelsel, richtingscoëfficiënten, de stelling van Pythagoras. En in feite is dit alles wat je nodig hebt om de meeste goniometrische opgaven op te lossen. Wellicht ligt de (drie)hoek niet mooi op de oorsprong van het assenstelsel, of heeft de schuine zijde van de driehoek niet mooi de lengte 1, maar in zulke opgaven is de driehoek gewoon een beetje verschoven, gedraaid en wat opgeschaald.
Grotere driehoeken
In de meeste opgaven heeft de schuine zijde van de driehoek niet precies de lengte 1, dus laten we eens kijken hoe we dat aanpakken. Stel je komt een opgave tegen met een rechthoekige driehoek:
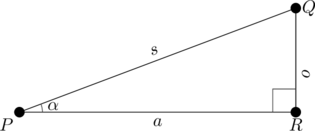
Deze driehoek lijkt erg op de driehoek in de eenheidscirkel. Het enige verschil is dat de schuine zijde van deze driehoek niet de lengte 1 heeft, maar de lengte \(s\). Dat betekent dat we de formules die we bij de eenheidscirkel hebben geleerd kunnen gebruiken, maar dat alles met een factor \(s\) schaalt. Dus:
\[o = s \cdot \sin \alpha\]
\[a = s \cdot \cos \alpha\]
Meestal leer je deze formules op een iets andere manier in je wiskunde boek:
\[\sin \alpha = \frac{o}{s}\]
\[\cos \alpha = \frac{a}{s}\]
Merk op dat de richtingscoëfficiënt van schuine zijde niet schaalt met een factor \(s\): het lijnstuk is langer, maar heeft nog steeds dezelfde richting. Dus er geldt nog steeds dat: \[\tan \alpha = \frac{o}{a}\]
Deze formules worden vaak geleerd als Sinus is Overstaande zijde gedeeld door Schuine zijde, Cosinus is Aanliggende zijde gedeeld door Schuine zijde, en Tangens is Overstaande zijde gedeeld door Aanliggende zijde (ezelsbruggetje: SOS CAS TOA).
Omdat de schuine zijde niet altijd schuin staat in een opgave (als de driehoek bijvoorveeld is gedraaid) wordt de “schuine” zijde tegenwoordig vaak de “lange” zijde genoemd, aangezien het de langste zijde van de driehoek is. Vandaar dat ook wel het ezelsbruggetje SOL CAL TOA wordt gebruikt.
Dit zijn de formules die je waarschijnlijk in je wiskunde boek staan en waarvan verwacht wordt om ze uit je hoofd te leren. Dat kan zeker geen kwaad; het is handig om ze paraat te hebben en meteen te kunnen gebruiken. Ik hoop echter dat het plaatje met de eenheidscirkel, en de uitleg daarbij je een beter beeld geven waar deze formules vandaan komen, en het gemakkelijker maakt om ze te onthouden.